Suppose we look at historical returns for two stocks and get something like Figure 1, for each. On the basis of the histogram and playing with various normal, lognormal etc. fits to the historical data, we conclude that, say a Normal distribution will adequately describe the returns. >What's Figure 1a? The distribution of about a thousand daily returns for GM stock and we'll assume they're normally distributed and ... >That's the red curve? Yes, it's a Normal distribution with the Mean and Standard Deviation of the historical returns. >It's a lousy fit! It doesn't matter. This is just an illustration of what to do with Copulas.

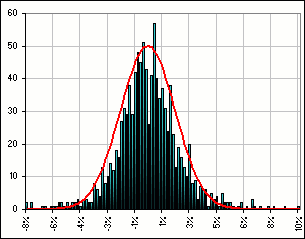Figure 1a

>Huh?
Instead of using the returns x and y, we use u and v where Figure 1b shows how the u-value is obtained from the x-value.

>I assume that Figure 1b is obtained from Figure 1a. Yes. Fig. 1a is the density distribution and Fig. 1b the associated cumulative distribution. Note that, although the x-values can be anything, the u-values lie in [0,1] and are uniformly distributed. Remember, by "uniformly" we mean that there is the same probability of selecting a u-value in [0.01, 0.02] and there is in selecting a value in [0.02, 0.03] or [0.75, 0.76] or ... >Yeah, I get it. It depends upon the size of the interval. Yes. Instead of Figure 1a, the density distribution of u's would look like this:

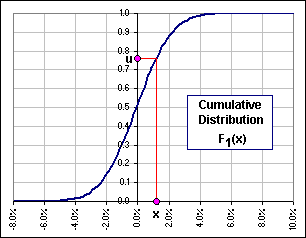Figure 1b

>I get it!
Good for you.
Now that we have uniformly distributed variables (our u and v variables) we need to pick a nice Copula.
We have several choices ... some of which we've already mentioned:
>That's it?
Notice that the C(u,v) uv as d some magic value (like 0 or 1, depending upon the copula).
>Yeah, so?
That'd be the case if the variables were independent. In other words, as d moves away from the magic value, the copula introduces more dependence.
>That's it?
For now ...

Examples

Let's look at the Clayton copula. We could do this:

1. Pick a thousand numbers u at random in [0,1] ... using Excel's RAND() function.
2. Determine the corresponding v-values, using the Clayton copula ... with some prescribed d-value.
3. Plot v versus u and calculate the Pearson correlation for the thousand pairs (u,v).

>Huh?
If we plotted just v versus u, all the dots would lie in a square with sides of length "1".
Using Excel's NORMSINV, we're assuming the "marginal distributions" of u and v are standard normal ... with Mean=0, SD=1.
Then the values would lie, mostly, in [-4,4] (that's 4 standard deviations from the Mean)... with just a few outliers.

Anyway, we'd get scatter plots like so:

   

>What'd the plot look like when you just did v vs u? Like Figure 2. See how they're all stuck in [0,1]? >And the correlation is the same, whether you assume normally distributed u's and v's or ... Or uniformly? Yes, that's the neat thing about copulas. You can use uniformly distributed u's and u's to get the correlation you want, then switch to whatever distribution you want for the two variables. That way you separate the correlation from the marginal distributions and ... >How do you do step #2, above? Given the u, get the corresponding Clayton v? Magic!

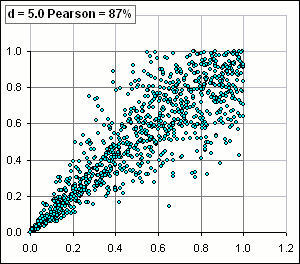Figure 2

Here's the Magic Ritual (using Clayton as an example):

1. Assume a copula C(u,v)
           C = [ u^-d + v^-d - 1 ] ^-1/d
2. Calculate the partial derivative ∂C/∂u and set w = ∂C/∂u
           w = u^-1-d [ u^-d + v^-d - 1 ] ^{-1/d - 1}
3. Solve w = ∂C/∂u for v in terms of u and w.
           v = [ w^-d/(1+d) u^-d - u^-d + 1 ] ^-1/d
4. Now pick u and w as uniformly distributed random variables on [0,1]   ... such as: u = RAND() and w = RAND(), in Excel
5. Then the v value associated with the selected u-value is given in step 3, above.

>And how do I know what the correlation will be? Suppose I want a 75% correlation, then ...? Okay, here's what I did: I picked some d-value. Then generated 5000 (u,v) pairs via the above Ritual and calculated the Pearson correlation. Then I repeated that Ritual for another d-value, and then another, then ... >And? And I got Figure 3. >So that chart tells me what d-value will give what correlation? I think so ... >You think so? Hey! Gimme a break! I'm just learning this stuff. >Are the numbers in Figure 3 supposed to agree with those in Figure 2? Sure? Why not? See the red dot? That's d = 5 and Pearson = 87%. >Aha! Just like Figure 2, eh? You got it.

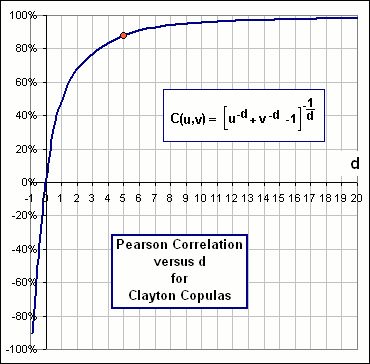Figure 3

>It'd be neat if you could do charts like Figure 3 for, say, Gumbo and ...
Gumbel? Yeah, okay, but ...

>And a spreadsheet would be good, and maybe Monte Carlo stuff with correlation given by some copula and then compare ...
Patience!

Okay, suppose we:

• Choose a Clayton copula and do the Magic Ritual to generate 1000 (u,v) pairs with a Pearson correlation of, say 87%
  ... so we choose d = 5.0 as suggested by Figure 3.
• Then we use the u-v pairs to generate x-y pairs with Mean[x] = 10% and SD[x] = 25% and Mean[y] = 7% and SD[x] = 10% where the x- and y-variables are normally distributed
  ... so, in Excel, we'd choose x = NORMINV(u, 0.10, 0.25) and y = NORMINV(v, 0.07, 0.10)
• Then we calculate the actual Pearson and Spearman correlations between the 1000 x-y pairs and the actual Means and Standard Deviations ...

>Just to see how close you came to what you wanted, right?
Exactly! Anyway, we'd get this:

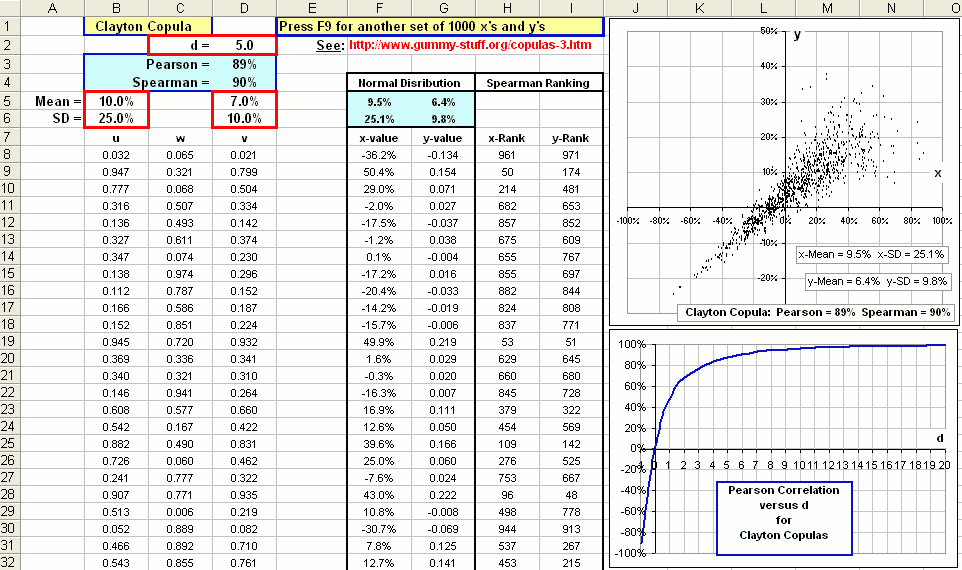
Click on picture to download

>Hey! You got a spreadsheet!
You think I'd do all this with pencil and paper?
We stick our prescribed Means and SDs into cells B5, B6 and D5, D6 and our chosen d-value in D2 ... hoping to get our 87%.
The u and w columns are just 1000 values of RAND() and v = [ w^-d/(1+d) u^-d - u^-d + 1 ] ^-1/d ... and we get a new set of 1000 each time we press F9 to recalculate.
The x and y columns are calculated using NORMINV( ) ... as we noted above.
The actual values of Pearson and Spearman and Means and Standard Deviations are shown in the blue cells.

>But you wanted 87% Pearson and you got 89%!
Nobody's perfect

>How about good ol' Frank? You just did Clayton and I think ...
The spreadsheet has Frank, too. It looks like this:

>And Gumbo?
Uh ... well, there's a wee bit of a problem with Gumbo Gumbel because of the problem in finding an inverse and ....

>Huh?
See copula math.

for Part IV