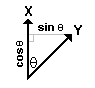|
We'll refer to variables x, y and z, each selected at random from some distribution.
(The distributions for x, y and z may or may not be the same.)
We'll refer to the Mean (or average) and Standard Deviation (or volatility) of the variables as (for example) M[x] and S[x].
(M[x], M[y], M[z] and S[x], S[y], S[z] may or may not be the same.)
1: M[x + y] = M[x] + M[y] ... the Mean of a Sum is the Sum of the Means
and M[x+C] = M[x] + C if C is a constant
and M[Cx] = CM[x] if C is a constant
|
|
By definition, the Variance of the x-variable is VAR[x] = S2[x].
Further, by definition:
2: VAR[x] = S2[x] = M[(x-M[x])2] = the average of (the deviation of x from its Mean)2
and VAR[x+C] = VAR[x] if C is a constant
and VAR[Cx] = C2VAR[x] if C is a constant
|
Increasing (or decreasing) M[x] shifts the distribution to the right (or left).
S[x] is a measure of how far the x-values vary from the mean, M[x]. (See Figure 1.)
| 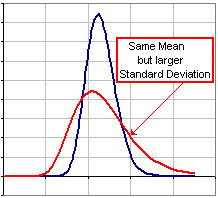
Figure 1 |
By definition, the CoVariance of the x and y variables is given by:
3: COVAR[x,y] = M[(x-M[x])(y-M[y])] = the average of (the deviation of x from its Mean)*(the deviation of y from its Mean)
so VAR[x] = COVAR[x,x] |
4: COVAR[x,y] = M[xy] - M[x]M[y] = COVAR[x+C,y]
so that adding a constant to either x or y (or both) doesn't change COVAR[x,y]
Further: M[xy] = M[x]M[y] + COVAR[x,y]
Also
COVAR[x1+x2+...+xn,y] = COVAR[x1,y]+COVAR[x2,y]+...+COVAR[xn,y]
If the variables have zero covariance (are "uncorrelated"), then
M[xy] = M[x]M[y] |
|
COVAR[x,y] | = M[(x-M[x])(y-M[y])] using 3
| | = M[xy - xM[y] - yM[x] + M[x]M[y]]
| | = M[xy] - M[x]M[y] - M[y]M[x] + M[x]M[y] using 1
| | = M[xy] - M[x]M[y] **
|
Further
|
COVAR[x+C,y] | = M[(x+C)y] - M[x+C]M[y] using **
| | = M[xy+Cy] - (M[x]+C)M[y] using 1, where M[x+C] = M[x]
| | = M[xy]+M[Cy] - (M[x]+C)M[y] again using 1
| | = M[xy]+CM[y] - M[x]M[y] - CM[y] = M[xy] - M[x]M[y]
|
Further
|
COVAR[x1+x2,y] | = M[(x1+x2)y] - M[x1+x2]M[y]
| | = M[x1y+x2y] - (M[x1]+M[x2])M[y]
| | = M[x1y]+M[x2y] - M[x1]M[y]-M[x2]M[y]
| | = M[x1y]-M[x1]M[y] + M[x2y]-M[x2]M[y] = COVAR[x1,y]+COVAR[x2,y]
|
Further
COVAR[x1+x2+...+xn,y] = COVAR[x1,y]+COVAR[x2,y]+...+COVAR[xn,y]
By definition, the Pearson Correlation between the x and y variables is given by:
| 5: PEARSON[x,y] = r(x,y) = COVAR[x,y] / (S[x] S[y] ) |
| 6: VAR[x] = M[x2] - M2[x] |
|
VAR[x] = COVAR[x,x] = M[x2] - M2[x] from 3 and 4
|
| 7: VAR[x+y] = VAR[x] + VAR[y] + 2 COVAR[x,y] = VAR[x] + VAR[y] + 2 r(x,y) S[x]S[y] |
|
VAR[x+y] | = M[(x+y-M[x]-M[y])2] using 1 and 2
| | = M[(u + v)2] where u = x-M[x] and v = y-M[y]
| | = M[u2] + M[v2] + 2 M[uv] = M[(x-M[x])2] + M[(y-M[y])2 + 2 M[(x-M[x])(y-M[y])]]
| | = VAR[x] + VAR[y] + 2 COVAR[x,y] using 2 and 3
|
|
VAR[x1 + x2 +...] | = M[(u1 + u2 + ...)2] where, as above, u1 = x1-M[x1] etc.
| | = M[Σuk2] + 2 M[Σukuj] k < j in the latter sum
| | = ΣVAR[uk] + 2 ΣCOVAR[uk, uj]
| | = ΣVAR[xk] + 2 ΣCOVAR[xk, xj] using 2: VAR[x-C] = VAR[x] with C = M[x] ... and using 4
|
8: if r(x,y) = 0 (that is, x and y have zero correlation) then
VAR[x+y] = VAR[x] + VAR[y]
and M[xy] = M[x]M[y] the Mean of a Product = the Product of the Means |
Put r(x,y) = 0 in 7 and COVAR[x,y] = 0 in 4.
9: if r(x,y) = 1 (that is, x and y have perfect correlation) then
S[x+y] = S[x] + S[y] the Volatility of a Sum = the Sum of the Volatilities |
|
VAR[x+y] = S2[x+y] | = S2[x] + S2[y]+ 2 S[x]S[y] using 7 with r(x,y) = 1
| | = (S[x]+S[y])2
|
|
so S[x+y] | = S[x] + S[y] if r(x,y) = 1
| | and, similarly, S[x+y] | = |S[x] - S[y]| (the absolute value) if r(x,y) = -1
|
10: if r(x,y) = 0 (that is, x and y have zero correlation) then
M[xy] = M[x]M[y]
VAR[xy] = M2[x]VAR[y] + M2[y]VAR[x] + VAR[x]VAR[y] |
|
M[xy] | = M[(x-M[x]+M[x])(y-M[y]+M[y])] adding & subtracting the Means
| | = M[(x-M[x])(y-M[y])+M[x](y-M[y])+M[y](x-M[x])+M[x]M[y]] multiplying
| | = COV[x,y]+M[x]0+M[y]0+M[x]M[y]] using 1 and the fact that M[x-M[x]] = 0
| | = COV[x,y] + M[x]M[y]]
| | = M[x]M[y]] if COVAR[x,y] = 0
| | VAR[xy] | = M[x2y2] - M2[xy] using 6
| | = (M[x2]M[y2] + COVAR[x2,y2]) - (M[x]M[y] + COVAR[x,y])2 using 4 (for each term)
| | = M[x2]M[y2] - (M[x]M[y])2 setting correlations (or CoVariances) to 0
| | = (M2[x] + VAR[x])(M2[y] + VAR[y]) - M2[x]M2[y] using 6, again!
| | = M2[x]VAR[y] + M2[y]VAR[x] + VAR[x]VAR[y]
|
11: if r(x,y) = 0 (that is, x and y have zero correlation) then
COVAR[x,xy] = VAR[x]M[y] |
|
COVAR[x,xy] | = M[x2y] - M[x]M[xy] using 4
| | = M[x2]M[y] - M[x](M[x]M[y]) using 8 (Mean of Product = Product of Means) when correlations are zero
| | = (M2[x] + VAR[x])M[y] - M2[x]M[y] using 6
| | = VAR[x]M[y]
|
If
r(x,y) = Pearson Correlation between variables x and y
Σ x stands for x1 + x2 + ... + xn
Σ xy stands for x1y1 + x2y2 + ... + xnyn
M[x] = (1/n) Σ x = the Mean of the xs
SD2[x] = (1/n) Σ (x - M[x])2 = (1/n) Σ x2 - M2[x]
their Variance or (Standard Devation)2
Beta[x,y] = slope of the regression line, plotting (xk,yk)
Error = the mean square deviation of the yk from the regression line
then:
r = {M[xy]-M[x] M[y]}/{SD[x]SD[y]}
= (1/n) Σ (x-M[x]) (y-M[y]) / {SD[x]SD[y]}
Beta[x,y] = COVAR[x,y] / SD2[x] = r SD[y] / SD[x]
Error2 = SD2[y] (1-r2)
If
X is the vector with components (xk - M[x]) / SD[x]√n
Y is the vector with components (yk - M[y]) / SD[y]√n
then
X and Y are of unit length. That is: ||X|| = ||Y|| = 1
r = X Y = ||X|| ||Y|| cos(θ) = cos(θ) Y = ||X|| ||Y|| cos(θ) = cos(θ)
Error = SD[y] |sin(θ)|
and
Y = ( cos(θ) + isin(θ) )X
= exp(iθ) X
where i rotates a vector by 90 degrees
(in the plane of X and Y ... so i2 = -1).
| 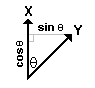 |
| 
If the weights of our portfolio are described by the n-vector W
and the covariance is described by the n x n matrix Θ,
then the Standard Deviation is the positive scalar σ, where:
σ2 = XT Θ X
See:
R-squared
Correlation Stuff
Linear Regression
|
|
|

 Y = ||X|| ||Y|| cos(θ) = cos(θ)
Y = ||X|| ||Y|| cos(θ) = cos(θ)