Sharpe ratio ... and related stuff.

In an interesting paper (in .PDF format), Victor Norton (Bowling Green State University) considers variations on the Sharpe Ratio in order to decide when to switch allocations from one set of assets to another and ...
>Sharpe Ratio?
Yes. If your average portfolio return is R and a risk-free return is Ro (for example, cash or money market), then the excess is r = R - Ro.
That excess is what you get for accepting the risk associated with the risky assets in your portfolio.
It's your Reward and you'd expect R to be greater than Ro (unless your portfolio is entirely in risk-free assets).

>That r is the Sharpe Ratio?
Not yet.
If the Volatility or Standard Deviation (SD) of your portfolio is small, then you should be happy. Chances are you'll get the Reward r. On the other hand, if your portfolio assets are volatile (so SD is large) then there's a good chance you may get a return less than the risk-free return, Ro.

The Sharpe Ratio measures Reward/Volatility, that is
Sharpe Ratio = r / SD = (R - Ro) / SD
>So the red graph is better, eh?
It'll have a larger Sharpe Ratio, if that's what you mean. That's because the Volatility = SD is small.
>But both the red and blue guys have the same Reward, eh?
Yes, because they have the same Mean (or Average) Return R.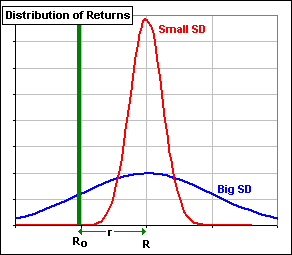


Figure 1

>So what does Norton do? Maximize the Sharpe Ratio?
Not exactly. The question is: What to use as the Portfolio Return R?
>You said it was the Average Return, so why not just ...?
But there are averages and averages. For example, if the returns over the last N months were R1, R2, ... RN, where R1 is the most recent and RN the most remote (N months ago), then the average ...
>It's (1/N)(R1+R2+ ...+RN), right?
That's one kind of average; the garden variety Arithmetic Mean. However, the are lots of Weighted Averages.
For example, you may want to place more weight on the more recent returns. In general, if you want a Weighted Average of N returns, then:

  • Pick N weights w1, w2, ... wN which add to "1" (that is, w1+w2+ ...+wN=1)
  • Calculate a Weighted Average = w1R1 + w2R2 + ... + wNRN.
  • Note that, if all returns are equal to, say, R, the Weighted Average = w1R+w2R+...+wNR = R
    which explains why the weights must add to "1".
Now the problem is to select the "best" weights.
>What's "best"?
Aah, that's the question, but ...
>And what if your portfolio has several assets? What's the "best" allocation then?
Okay, but first consider the weighted average ritual with a single stock (or mutual fund):
  • If r2, ... rN are the monthly rewards ... meaning: (monthly stock return) - (monthly risk-free return), then
  • rav = W1r1+W2r2+...+WNrN is the weighted average reward (for that stock).
  • If we let w1 = SQRT[W1], w2 = SQRT[W2], etc. be the Square Root of the weights, then sum of products can be written as
    rav = w1(w1r1)+w2(w2r2)+...+wN(wNrN)
  • Following Norton, we introduce a vector E with N components w1, w2, ... wN:   E = [w1, w2, ... ,wN]
  • The length of this vector is ||E|| = SQRT(w12+w22+...+wN2) = SQRT(W1+W2+...+WN) = SQRT(1) = 1
    (since the weights add to "1"). Hence E is a unit vector.  
  • In addition, we introduce another vector: r = [w1r1,w2r2,...,wNrN].
  • With these two vectors we can write the (weighted) average stock reward as a dot product (or scalar product):
    rav = Er   (meaning we add the product of components of E and r)

>Huh?
If these two vectors, E and r, were 2-dimensional, they might look like Figure 2A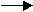  

The DOT product gives the (product of their lengths)*(the cosine of the contained angle):
rav = Er = ||E|| ||r|| cos(A)
But since ||E|| = 1, then the DOT product gives the component of r in the direction of the vector E.

Further, the vector r is the sum of two vector:
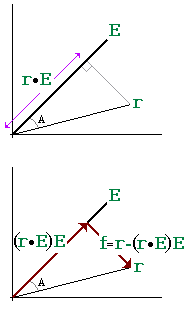one in the direction of E with length Er ... and that can be written as (Er)E
And the difference between this vector and r itself ... as shown in Figure 2B.


Figure 2A and Figure 2B

To start, let's consider a portfolio with just two assets:

  1. Rk,1 and Rk,2 are the monthly returns for assets 1 and 2 (with k = 1, 2, ... N) and Ro is some Risk-free Return.
  2. rk,1 and rk,2 are the monthly Rewards for assets 1 and 2 where rk,1 = Rk,1-Ro and rk,2 = Rk,2-Ro.
  3. rav,1 = ΣWkrk,1 and rav,2 = ΣWkrk,2 are the Weighted Average Rewards for each asset.
  4. If we devote fractions x and y to each asset (where x + y = 1) then the monthly Portfolio Rewards are
    Pk = x rk,1 + y rk,2   (k = 1, 2, ... N)
    and the Weighted Average Portfolio Reward is
    Pav = ΣWkrk = ΣWk(x rk,1 + y rk,2) = x rav,1 + y rav,2
    and the monthly deviations from this average are
    Pk - Pav = x (rk,1-rav,1) + y (rk,2-rav,2)   (k = 1, 2, ... N)
  5. Our Standard Deviation of the Portfolio Rewards is then given by the Weighted Average of the squares of these deviations, via::
    SD2 = ΣWk[Pk-Pav]2 = ΣWk[x (rk,1-rav,1) + y (rk,2-rav,2)]2
  6. We take as our Portfolio Sharpe Ratio:
    Sharpe Ratio = Pav / SD
  7. The (Weighted) Standard Deviations of the asset rewards are SD1 and SD2 where
    SD21 = ΣWk[rk,1-rav,1]2 and SD22 = ΣWk[rk,2-rav,2]2