I was recently reading Bernstein's Frontier article and got to thinking.

>Now that was a mistake.
Pay attention.

It is customary to say that an investor who takes on more Risk expects higher Returns.
It is also customary to define Risk as Standard Deviation or Volatility.

>And what's the Reward, as in Risk / Reward Ratio?
Often, it's taken as simply the Return on our Portfolio, so we would say:

(1)       Risk/Reward = (Standard Deviation)/(Portfolio Return)

Or, the Reward might be the Return on our Portfolio, over and above some risk-free rate, so we would say:

(2)       Risk/Reward = (Standard Deviation)/(Portfolio Return - RiskFree)

The reciprocal of the Ratio in (2) is called the Sharpe Ratio.

In Part I we saw that the Standard Deviation increases (sort of) as the square-root of the time period.
However, our Return, over longer and longer periods of time, increases more dramatically.

For example, suppose:

• Our annualized Portfolio Return was 8%
  so our Portfolio would grow according to (1.08)^N , over N years
• The annualized Standard Deviation (or Volatility) of our Portfolio was SD = 20%
  so this would grow as the years progressed as 0.2 SQRT(N) (according to that square-root-of-time stuff)
• The Ratio would be: SD / Return = 0.2 SQRT(N) / (1.08)^N
  which would look like this:
  
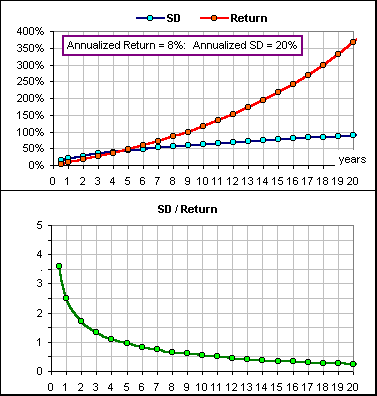
  Figure 1

>I assume it's not that smooth in real life, eh? True. >If you used the actual return, over umpteen years, what'd it look like? If I used the actual cumulative return and used that square-root increase in Standard Deviation I'd get this: 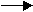>But I thought that square-root stuff was okay for short periods of time and you're talking here about mega-years. Yes, you're right. So let's do it again with ... >Hold on! I thought you didn't like using Risk = Standard Deviation. I don't, so let's change it.

This is what we'll do:

• We'll define Risk as the Probability that our annualized Portfolio Return, R, is less than, say 3%.
• We'll define Reward as the Probability that R is greater than, say 8%.
• We'll then consider the Ratio: Risk / Reward = Probability(R<3%) / Probability(R>8%)

>What's so special about 3% and 8%?
Nothing. It's just an example. We might consider 3% as some risk-free return or maybe inflation, so our Risk is the probability of getting a Return less than inflation. If we get a return greater than 8% we'd be ecstatic. That's a real return of 5% above a 3% inflation rate. That's our Reward, but it's a personal thing. You plug in whatever numbers you like.

>So?
So let's investigate:

First we'll assume that our Returns are Normally distributed with Mean M and Standard Deviation S. The cumulative distribution looks like so in the case M = 8% and S = 20%. The cumulative distribution gives the probability that a return is less than any given number. In this case we're looking at the probability that a return is less than 3% (that's the red arrow: 0.39) and less than 8% (the green arrow: 0.50). The probability that a Return R is greater than 8%, namely Probability(R>8%), is then 1 - Probability(R<8%).

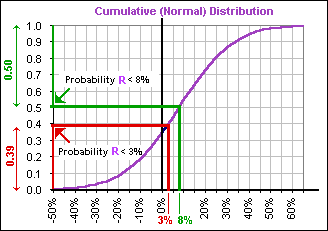Figure 2

Our Risk/Reward Ratio can then be written:

For the case illustrated in Figure 2, it's 0.39/0.50 = 0.78 (which is ratio of the two double-arrow lengths illustrated in the Figure: the red divided by the green).

In general, for a Normal distribution of Returns, we get the Magic Formula:

Probability(R < a) / { 1 - Probability(R < b) } =

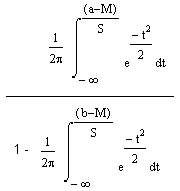
>What! You gotta be kidding! I think ...
Wait! I just wanted to illustrate that, mathematically speaking, this particular Risk/Reward Ratio depends upon two numbers,
(a - M)/S and (b - M)/S, where "a" and "b" are returns. Do you recognize this format?
>Are you kidding?
They're Sharpe Ratios, as we saw in equation (2), above.
>Yeah, but why don't you just show a picture or two?
Okay, here's a picture:

We start in 1950 and

• Determine the Mean of the 1-year Returns, then the Mean of the 5-year Returns, then 10-year, etc.
• Determine the Standard Deviation of 1-year, 5-year, 10-year etc. Returns.
• Assuming these Returns are Normally distributed, calculate the Risk/Reward Ratios for 1, 5, 10, etc. years using the Magic Formula above.

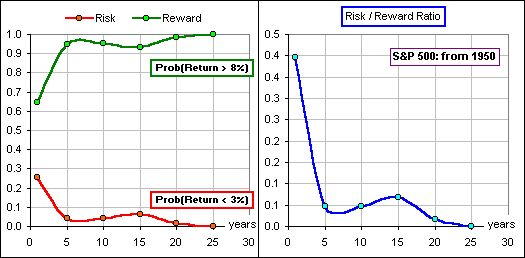
Figure 3

• We'll look at all the 1-year Returns, 2-year Returns, 3-year Returns etc. and see which ones were less than 3%, then calculate the sum of the absolute value of the deviations from 3%:
  That is, for all Returns R < 3% we calculate Σ | R - 3 |
  (This gives us our measure of Risk where the really BAD returns are weighted more heavily than those just under 3%.)
• Similarly, we look at all the 1-year Returns, 2-year Returns, 3-year Returns etc. and see which ones were greater than 8%, then calculate the sum of the absolute value of the deviations from 8%:
  That is, for all Returns R > 8% we calculate Σ | R - 8 |
  (This gives us our measure of Reward.)
• Then we calculate the Ratio of these two numbers, Risk / Reward, for 1-year, 2-year, 3-year etc. Returns.

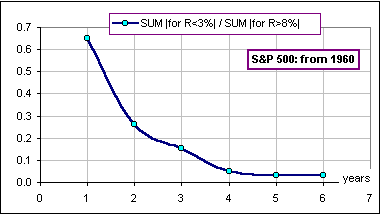
Figure 4

>Boring.
Yes. It doesn't take long for this Risk/Reward Ratio to become negligible.

>So what do you conclude about Risk / Reward Ratios?
It don't matter how you slice it, the longer you wait the smaller it gets and ...

>And it don't hardly matter which one you use!
Yes, but it's perhaps more interesting to compare Risk/Reward Ratios for different asset classes. We've been doing the
S&P 500, but how do the Ratios compare for Large Cap Growth stocks or Bonds or ...

>So, do it!
Well, to start with, we can do Large and Small Cap Growth and Value Indices and our friend the S&P 500 and the Total Stock Market ...

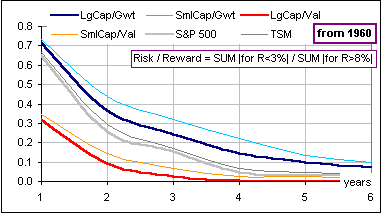
Figure 5

>Are we looking for the smallest Risk-Reward Ratio?
Why not?
>I'll take Large Cap Value!
How about adding some bonds or maybe ...
>Picture?

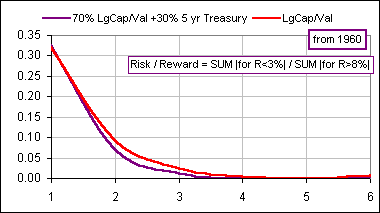
Figure 6

to continue