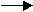| Predicting Markets ... and P/E Ratios: a continuation of Part I |
We're talking about the stock market ... and randomness ... and predictability ... and ...
>Yes, I know ... please continue.
Okay. We'll consider the S&P 500 Index as representative of "The Market".
We expect a correlation between the current P/E Ratio and future market returns.
Here's a picture:
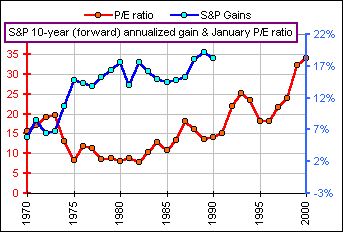
Figure 1
- We write down the P/E Ratio for, say, January, 1970.
- We compute the annualized market return over the next N = 10 years.
- We repeat steps (1) and (2), starting in January, 1971 then January, 1972 etc. etc.
each time noting two numbers:
the P/E Ratio for January of that year and the Annualized Return over the subsequent N = 10 years. - When we get to the present day, we stop (because the data ends!) and calculate the Pearson Correlation between these two seqences of numbers.
>Why?
Well, to see if the P/E Ratio is a predictor of future market returns. To see if there's a
correlation between today's P/E Ratio and tomorrow's markets. To see if ..
>Okay, I get it. One might expect, say, if today's P/E is high then the market is overpriced ...
And future market returns will be less. Yes. A negative correlation.
When P/E is up, the market will go down. When P/E is down, the market will go up.
That's what we'd expect ... as in Figure 1.
>But why January of each year? And why N = 10?
The month isn't important. We could take any month or the average P/E for the year or some
other measure of current P/E. I just want to explain a certain ritual. As for N = 10,
we'll repeat steps (1) - (4) with N = 3 then N = 4 then N = 5 etc. etc.
|
>And the result of all this?
>But it gets more negative as N increases.
>Wow! 15 years and we've got us a 90% correlation!
| 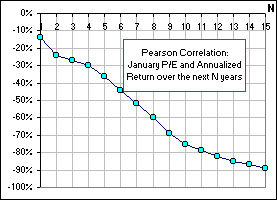 Figure 2 |
|
>So, is that a good predictor of future market returns?
Here's another picture, in Figure 3, showing the "current" P/E Ratio and the Annualized Return (over the subsequent 15 years) ... starting in 1970 then 1971 etc. and ending in 1985 (because my 15-year data ends). It suggests that, when the P/E increases by "1", the (annualized) return over the next 10 years will decrease by 0.59% (the slope of the regression line ... or, equivalently, the beta). >I'd say you've got something there! Look at that correlation in Figure 2! Can I show you one more picture? >Why not? |  Figure 3 |
|
Doesn't it seem strange to you that anybuddy might want to use the current P/E, like in January 1970, to say something about the next 10 years worth of returns? That the longer the time period, the longer we peer into the future, 15 or 20 or 30 years ... the better the correlation? Doesn't that seem strange? >You're trying to tell me something, right?
>Don't tell me! It's the TSE, eh? Another stock index, right?
| 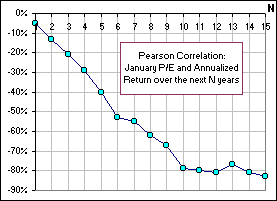 Figure 4 |
So I don't think that the remarkably high correlation between current P/E and 15-year future returns is a result of P/E being an excellent long term predictor. Indeed, the correlation gets better (meaning closer to -100%) for 20 years and 25 years, yet the returns I generated are random. I don't think that the actual P/E is a good predictor of randomly generated returns.
>Yeah ... so?
So I think it's more a mathematical phenomenon rather than P/E and Return correlation.
The P/E ratios are likely to have a higher and higher correlation with any set of
random variables if the number of random variables increases ... as it would if we consider
10 then 15 then 20 years worth, for example.
>And that always happens?
Uh ... no, not always, but I can choose an appropriate Mean and Standard Deviation and
select a bunch of random returns (from a Normal distribution with the selected Mean and SD)
then get the correlation between the actual P/E ratios and N phantom
returns, "annualized". Usually, if the selected Mean is positive, the correlation
decreases as N increases ...
>Usually? Have I ever told you that a picture is worth a thousand ...
Okay, here's a few examples of randomly selected returns, where N runs from 5 to 10:

Figure 5
>Can you prove anything?
Well ... mmm ... give me time.
In the meantime, remember that the Pearson correlation between
two sets of numbers, say {x}
and {y}, is ...
>Who are {x} and {y}?
I'm using {x}
to represent a set x1, x2, x3 etc. and I'll also
use M(x) to stand for the Mean of the set:
M(x) = (1/N){
x1+x2+x3+...+xN
}
and
M(xy) = (1/N){
x1y1+x2y2+...+xNyN
}
and SD(x) is the Standard Deviation of the set {x}.
Anyway, the Pearson correlation is: r = [ M(xy) - M(x)M(y) ] / [ SD(x) SD(y) ]
If the set {x} has some probability distribution, then M(x) is the expected value of the randomly selected x. The more x's you select, from this set, the closer the average will be to this Mean. It's like tossing coins with sides valued at 0 and 1. In ten tosses, you could get ten 1s with a Mean of 1. However, the Mean of the values, as the number of tosses increases, is 1/2.
>Half 0s and half 1s, eh?
Yes. So we'd expect that, for example, as we select a greater number of returns, their Mean
(and, also, their SD) will approach some limiting value.
>Precisely?
Well ... approximately. We're talking randomness here.
>You wouldn't happen to have a ...?
Yes. Here's some pictures where we do the (1) - (4) steps above, but using the monthly
S&P returns and P/E (so we get lots of points, from 1970). Notice that the Mean and
Standard Deviation sort of level out as the number of months increases from 5 to 180. One would
then expect some limiting value for the Pearson correlation
... which could very well be quite negative.
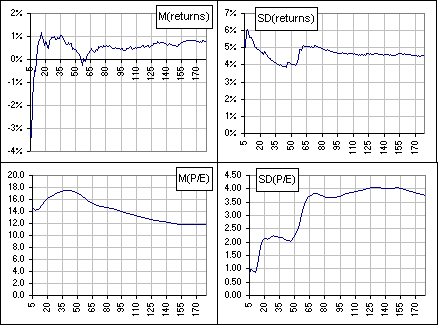
Figure 6
>So?
So, it'd be nice if there were some optimal time period, say 2 or 3 years,
where the annualized return was greatly influenced by the current P/E Ratio. Unfortunately,
I don't think that this Pearson correlation stuff will identify an optimal time period.