Omega Geometry

The definition is:

We consider the case where F(x) = 0 for x < L and F(x) = 1 for x > U ... so f(x) = F'(x) = 0 outside (L,U).

Then (from part I): Omega = 1 + [C - r ] / A[L,r] where r is some return   between the Minimum and Maximum return L and U are the Lower and Upper limits on returns   the Minimum and Maximum return A[L,U] is the area under the cumulative distribution of returns   from the Minimum to the Maximum C = U - A[L,U]   which, for a given stock and time period, is a constant.

Let f(x) be the probability density for a set of returns ranging from r = L to r = U. (Remember, outside of this range, f(x) = 0.)
The cumulative distribution F(x) is:

F(x) = f(y)dy = f(y)dy Further, A[L,r], the area beneath F(x) from L to r, is then: A[L,r] = F(x)dx = f(y) dy dx = f(y) dA where the integration is over the region shown.

Interchanging the order of intregration we get:   f(y) dy dx = (r - y) f(y) dy

Hence:

[1]     A[L,r] = F(x)dx = (r - x) f(x) dx

>You realize you could get [1] using integration by parts?
Okay, let's do that.

In general, we may write:   A[a,b] = F(x)dx = F(x) x - f(x) x dx   integrating by parts

Hence:

[2]     A[a,b] = b F(b) - a F(a) - x f(x) dx

In particular:

[3]     A[L,U] = U - x f(x) dx   since F(U) = 1 and F(L) = 0

and

[4]     A[L,r] = r F(r) - x f(x) dx

Note that (a,b), the x-coordinate of the centroid of the area beneath y = f(x) from x = a to x = b, is given by: (a,b) f(x) dx = x f(x) dx and since f(x) dx = F(b) - F(a) then (a,b) = [1/(F(b) - F(a))] x f(x) dx

Since F(U) - F(L) = f(x) dx = 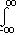f(x) dx = 1 we recognize x f(x) dx as the x-coordinate of the centroid for the total area beneath y = f(x) ... shown as a red dot in Figure 1. We'll call this simply . Hence, from [3]: [5]     A[L,U] = U -

Figure 1

>Centroid? is the Mean of the distribution!
I knew that!
Further, (a,b) is the average of the returns which lie between x = a and x = b.

We now rewrite the definition of Omega = 1 + [C - r ] / A[L,r]

First, note that C = U - A[L,U] = U - (U - ) =

Further, from [4], A[L,r] = r F(r) - x f(x) dx and F(r) is the area under f(x) from L to r (as shown in Figure 2). Hence (L,r) = (1/F(r)) x f(x) dx is the x-coordinate of this area ... the magenta dot in Figure 2. We can then write: A[L,r] = F(r) ( r - (L,r) )

Figure 2

Finally, then, we have:

[6]     Omega = 1 + (1/F(r)) ( - r ) / ( r - (L,r) )

Note that Omega = 1 at the Mean Return:   r = .

Omega and Average Returns

We repeat the relationship between the area under y = f(x) and the average of returns, between x = a and x = b, namely:

[7]     (a,b) = [1/(F(b) - F(a))] x f(x) dx = the Average of returns which lie between "a" and "b"

We stare fondly at all the relationships from [1] to [7] and conclude that [6] can be rewritten like so::

>Did you really need all that bumpf above to get here? Wasn't there a shorter route?
We took the scenic route. Like it?
>No. Besides, isn't there a picture to go along with ... ?
Yes.