about Points of Inflection & Secants joining Critical Points
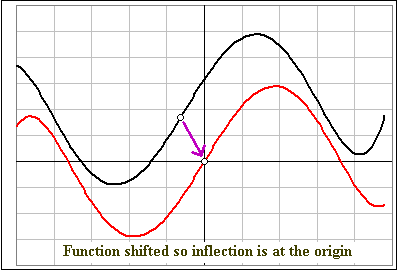
motivated by a discussion on the Calculus Forum

Without loss of generality, we assume that f(x) has a point of inflection at the origin: (0,0).

>Huh? Can you do that?
Sure.
We just shift f(x) left/right & up/down, without distortion, so that the point of inflection is moved to the origin.

Then, assuming f is twice continously differentiable, f ''(0) = 0.

Suppose, too, that f(x) is an odd function. That is, f(-x) = - f(x).

Then
y ' = f '(x) will be an even function. That is, f '(-x) = f '(x).

>Can you prove that?
Sure. Want to see the proof?
>No!


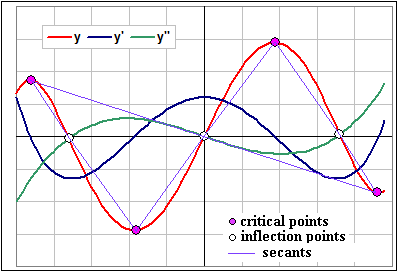
If y = f(x) has a critical point at x = c, then f '(c) = 0.
But then f '(-c) = f '(c) = 0 as well, so x = -c also gives a critical point.
That is, (-c, f(-c)) and (c, f(c)) are both critical points.

>So critical points are in pairs, on either side of the point of inflection at x = 0, right?
You got it. And they're also equidistant from the point of inflection.
The secant joining these two critical points is:   y = (f(c)/c) x
Note that it passes thru' our critical point at (0,0).

>A picture is worth a thousand ...
Here's a picture:
Note that we could move the function left/right & up/down so each point of inflection is at the origin.

>But you shifted things around. What if you left them where they were?
Then it'd look like this where we'll call the unshifted functions Y(x), Y '(x) and Y ''(x) :

Example:
Consider the cubic: Y(t) = A + B(t-a) + C(t-a)2 + D(t-a)3 where t = a gives a point of inflection.
Then Y ''(t) = 2C + 6D(t-a) = 0 at t = a.
Hence C = 0 and Y(t) = A + B(t-a) + D(t-a)3.
Now shift left/right & up/down and consider: Y(t+a) - A = y(x) = B x + D x3, an odd function with inflection at the origin.
>And what if, after you shift left/right & up/down so the inflection is at (0,0) ... what if the function isn't an odd fucntion?
Then all bets are off. For example, if we add k x4 to y(x) we'd get this: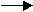
The new function, y(x) + k x4, has a point of inflection at the origin, yet the secant don't hardly pass thru' (0,0).
Of course, it'll depend upon our choice of k. We can choose k so that the critical points don't lie on any line through (0,0).

In fact, we can add other sexy functions to y(x), say k(x) where k ''(0) = 0, then y(x) + k(x) will still have (0,0) as a point of inflection.
Then we we can fiddle with k(x) so that anything can happen and we ...
>zzzZZZ

See Math Stuff