| a Title goes here ... and something else here |
>sidekick goes here
|  Figure 1 |
[1]
S f(tk)Dt
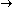  f(t) dt
as Dt f(t) dt
as Dt 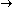 0 0
|
- Suppose returns r have a Mean M[r] and Variance V[r].
- If the returns r are lognormally distributed, then r = ex where the x's are normally distributed.
- Suppose the Mean and Variance for the x's are M[x] and V[x].
- Because of the lognormal association, the relation between M[r], V[r], M[x] and V[x] is
V[x] = log[1+V[r]/{1+M[r]}2]
M[x] = log[1+M[r])]- V[x]/2 - Hence eM[x] = (1+M[r]) e- V[x]/2 = (1+M[r]) [1+V[r]/{1+M[r]}2]-1/2
- The Median return is then r = eM[x] - 1 = (1+M[r]) [1+V[r]/{1+M[r]}2]-1/2 - 1
- For small M[x] and V[x], r is approximately
r = (1+M[r]) [1- (1/2)V[r]] - 1 which is approximately r = M[r] - V[r]/2.
|
EXP(m+s2/2) = M
EXP(2m+s2) [EXP(s2)-1] = S2 |
|
m = LOG(M) - s2/2
where s2 = LOG(1 + S2/M2) |

