| the Black-Litterman: Part II ... continued from Part I |
We suppose that a "Market Portfolio" is optimal and ...
>Huh?
By "Market Portfolio" (or, as it's usually called, the "Equilibrium Portfolio") we mean some portfolio which reflects the stock market, such as the S&P500 or maybe 60% S&P + 30% Bonds + 10% EAFE or maybe ...
>Yeah, but what's "optimal"?
|
I mean optimal weights, in the sense that if we make small changes in portfolio weights without changing the "Risk", we will not increase our returns.
In other words: With an Optimal portfolio, if we increase our return we will also increase our "Risk". >Yeah, but what's "Risk"? We'll adopt the standard definition: Risk = Standard Deviation. In Figure 1, for example, we're allocating fractions x1 and x2 to two of our assets. At the "Optimal" allocation, if we make small changes in allocation, we do not change the Standard Deviation. >Neither do we increase our returns, right?
| 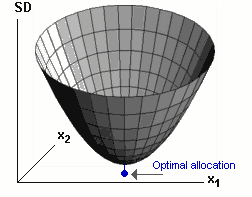 Figure 1 |
If the weights of our portfolio are described by the n-vector X and the covariance is described by the n x n matrix Θ, then the Standard Deviation is σ, where:
[1] σ2 = XT Θ X
Recall that the asset weights are the components of the vector X, namely x1, x2, ... xn.
Now suppose we change one of the weights, say xk.
The rate of change of σ (σ is our "Risk") is
∂σ/∂xk.
For sanitary reasons, we'll call this rate of change Δk. That is:
[2] Δk = ∂σ/∂xk
If we now sell a small amount of the kth asset, say δk,
the Risk (that's σ) will change by
-δk Δk.
(It's negative because we're selling.)
Because we changed the amount of the kth asset by -δk,
our return will change by -δk rk.
>Huh?
Remember: our portfolio return is x1r1 + x2r2 + ...+ xnrn.
The contribution to this return by the kth asset is xkrk.
Reducing xk by δk will reduce our return by δk rk.
For a small negative change in asset #k we have the resultant changes in SD and return, namely:
[3] Change in SD = -δk Δk and Change in Return = -δk rk.
We now change the jth asset by some small positive amount ... meaning that we buy some. By how much? By
[4] δj = δk Δk / Δj.
Our "Risk" will then change by δj Δj
= [δk Δk / Δj]Δj
= δk Δk.
In other words, this sell-then-buy scenario will change our "Risk" by -δk Δk + δk Δk = 0.
So our "Risk" σ will not change ... with these particular, small changes.
>Yeah, so we're at that blue point in Figure 1, but what about our return?
I'm glad you asked.
Because of the purchase of δj of the jth, our return will change by +δj rj.
The total change in return will then be: -δk rk + δj rj.
Using [4], this total change is:
= -δk rk + (δk Δk / Δj) rj
= δkΔk[-rk /Δk + rj / Δj ]
>I have no idea what you're ...?
Pay attention! If the ratio rj / Δj is different from rk / Δk,
then we sell the asset with the smaller ratio and buy the asset with the larger ratio.
That'd mean that the change in return, namely δkΔk[-rk /Δk + rj / Δj ],
is positive (since rj / Δj > rk / Δk).
>But what if you sell the asset with the larger ratio?
The point is this:
If there are two ratios, rj / Δj and rk / Δk,
which are different, then we can increase our return without changing our "Risk": σ
>So?
So an Optimal Portfolio cannot have different ratios. An Optimal Portfolio must have all these ratios equal!
>If you say so ...
Indeed, that characterizes an Optimal Portfolio ... so we give it a place of honour:
| For an "Optimal" Portfolio: rk / Δk = rk / ( ∂σ/∂xk ) = constant for all k = 1, 2, ...n |
>Didn't you say I could incorporate my own views of the market? What if ...?
Okay, let's do that ... since it's what makes Black-Litterman "special".
| the Black-Litterman Equation |
Our tack will be somewhat different than earlier. In particular, our notation!
We'll let μ be the n-vector of expected asset returns for the Equilibrium Portfolio (based, perhaps, upon historical data).
We let Σ be the covariance matrix for the Equilibrium Portfolio (EP).
>Why "equilibrium"?
The assumption is that "the Market" is in equilibrium, supply = demand, so the prices associated with the assets in such a portoflio are "fair value".
Okay. We now assume that the actual (future) returns for our EP are denoted by μ'.
They have μ as their Mean plus some random error:
[5a] μ' = μ + ε
where ε are the random deviations from the Mean
Further, we'll assume that the deviations, ε, are normally distributed with Mean = 0 and Covariance equal to τ Σ
(τ is some as-yet-unspecified scalar).
Then our portfolio will have asset returns which reflect our views of the market.
>Huh?
We might think:
"There's no way I can expect gold to behave in the near future as it's done in the past, and with all the unrest in the middle east, oil will undoubtedly ...
>Yeah, yeah. So I have my own views. So what?
So we write the expected returns of our portfolio as:
[5b] Q = P μ + η
where η are the random deviations from the Mean for our Portfolio.
where Q, an n-vector describing our asset returns has, for each asset, a Mean return which depends upon the EP asset Means (that's μ).
This association is described by the n x n matrix P whose rows contain weightings associated with each EP asset return.
In addition, of course, there's the inevitable random error η.
As we did above, we'll assume that the deviations, η, are normally distributed with Mean = 0 and Covariance equal to Ω
To rid ourselves of the errors (or "residuals") ε and η
we do the linear regression thing:
To this end we introduce matrices:
[5c]  where I is a unit matrix
where I is a unit matrix
so we may write:
[5d] y = X μ + u
That leads to a linear regression problem, namely: "Determine the best choice for μ".
Since the residuals ε and η have Covariances τ Σ and Ω respectively,
the column vector u has Covariance Ψ where:
[5f]  ... where 0 is a null matrix
... where 0 is a null matrix
Now recall something from Part I, namely the optimal allocation of assets will generate expected returns of:
[5g] E[X] = XTΨ-1X
The "best" choice of regression parameters is then (as noted in the linear regression tutorial):
[5f] μ = (XTX)-1XTY
 ... don't trust nothin' yet. I'm still trying to understand this stuff &#$#%@!?
... don't trust nothin' yet. I'm still trying to understand this stuff &#$#%@!? 
