another Distribution ... continued from here

Once upon a time we talked about a distribution of returns with Mean = m and Volatility = s, but one that'd give fatter tails and ...
>Is that your Mystery Distribution?
No. Here we want to consider yet another distribution of the form:
(1)       f(x) = A e-b SQRT( 1+k(x-m)2 )
where we need to choose the numbers A, b and k appropriately. In particular, to mimic the behaviour of some stock returns.

The cumulative distribution is determined by the area beneath the f(x) curve and denoted by:
      F(x) = f(u) du
>Huh?
The probability that x will be less than, for example, 5% is F(5) = 20% as shown on the right-most picture, in Figure 1.
>And that 20 is the area under the f-curve?
Yeah, the area to the left of x = 5%.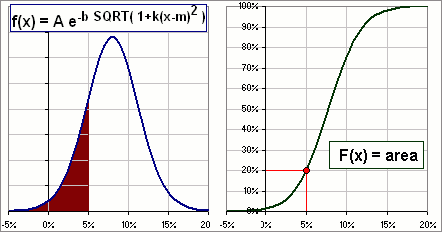

Figure 1
The probability that x is less than infinity is clearly 100% so we need to choose A, b and k so that:
      F(∞) = = 1
>Is it equal to "1" or "100%"?
They're the same: 1 means 100%.

Now we'll search for appropriate values for A, b and k.


Note that, when z is close to 0, SQRT(1+z) = (1+z)1/2 = 1+z/2 ... approximately.
So, when x is close to its Mean m, SQRT(1+k(x-m)2) = 1+k(x-m)2/2     (approx.)
so we can write f(x) as:
      f(x) = A e-b(1+k(x-m)2/2) = Ae-b e-bk(x-m)2/2 (approx.)
This is the form we'd expect since the Normal distribution has this form, namely:
      f(x)normal = 1/SQRT(2π) e-(1/2)(x-m)2/s2

In order to match these characteristics near the Mean, we set
        bk = 1/s2   or   b = 1/ks2

That gives:
(2)       f(x) = A e-1/ks2 SQRT( 1+k(x-m)2 )

Since we also want = 1   we choose A so that
      A e-1/ks2 SQRT( 1+k(x-m)2 )dx = 1

That makes A a function of k, so we'll write:
(3)       A(k) =
1

e-1/ks2 SQRT( 1+k(x-m)2 )dx

>But A depends upon the Mean and Standard Deviation as well, right?
Yes, but we know the numbers m and s ... assuming we're trying to mimic the distribution of returns for some particular stock.
>Altogether now?
Yes. Altogether now:
f(x) = A(k) e-(1/ks2)SQRT(1+k(x-m)2/2)
  where     A(k) =
1

e-1/ks2 SQRT( 1+k(x-m)2 )dx

>So what's k?
Like I said, we choose it so as to mimic the distribution of returns for some particular stock.
>Well, you're gonna have fun evaluating A, eh?
Not on a spreadsheet. Here's what we'll do:
  • We'll download daily stock prices for, say GE, and calculate the daily returns.
  • Then we'll plot the distribution of these returns, like Figure 2.
  • We'll look at the Normal and Lognormal distributions with the same Mean and Standard Deviation as the GE returns. There's little difference, for daily returns.
  • We'll note that the peak needs to be taller and we need fatter tails.
  • We'll then try out our "other distribution" with various k-values to see if we can improve upon this.

>Yeah, so?
Okay, if we consider the distribution of GE returns (as per Figure 2) and pick a nice k-value, we can get Figure 2A, below.


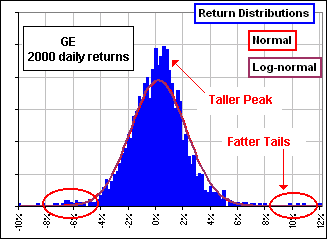Figure 2


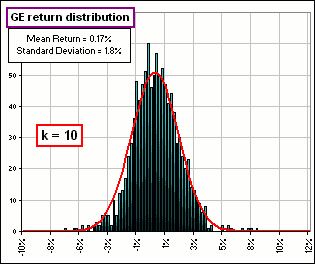Figure 2A

>Why k=10?

Actually (it surprised me!), the chart of f(x) is relatively insensitive to your choice of k.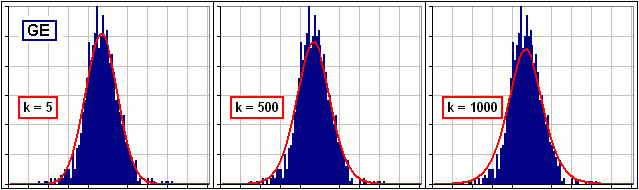


Figure 2B
>That peak may be relatively insensitive, but the tails ...
Aah, yes, the tails. I guess that's because we tried to match the actual distribution near the Mean - and that's near the peak.
But the tails, they're ... uh ...
>Fat!
Well, fatter, for large k-values, but the peak drops a bit. So we have to compromise between matching the peak and the tails.
Here's a few more:


Figure 2C

>Okay, but how do you evaluate A(k)?
You mean: e-1/ks2 SQRT( 1+k(x-m)2 )dx ?
I do a sum, like so, for a bunch of j's: Σ e-1/ks2SQRT(1+k(xj-m)2)Δx
>Huh?
Don't worry about it.

Remember when we noted that actual returns can sometimes be extreme ... far more (or less!) than one would expect from a Normal or Lognormal distributions.

(See this chart where the upper chart with the wild returns is real whereas the lower is fictitious, based upon a Normal distribution with the same Mean and Volatility.)
In Figure 3 (top chart) we have the daily returns for MSFT (for the past ten years).

If the distribution were Normal (for example) then, as it turns out, we'd expect a return outside the range -8% to 8% once or twice. In fact, there were ...

>I count 6!
Yes, me too. Six in this 10-year period.

On the other hand, if we try to mimic the MSFT returns using our OTHER distribution we can get lots of returns outside (-8%, 8%).

>And the match? I mean the actual distribution vs ...
I know what you mean ...


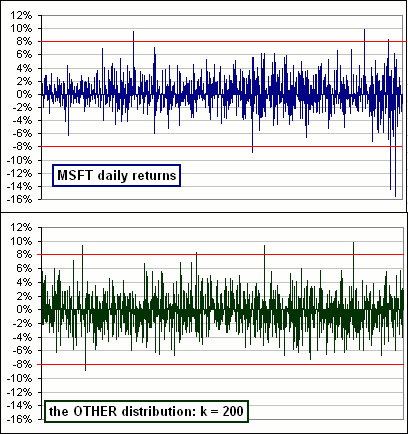Figure 3
>Why k = 200? You just pick a k which works, eh?
Yes, of course. What would you suggest?

>I'd suggest ... uh, picking a k which works. So, where's the spreadsheet?
I'm thinking about it ...

to continue