|
buy an Annuity after retirement?
This stuff is associated with This Stuff |
Here's the problem.
We're retired and want to know whether we should devote a fraction of our portfolio to an immediate, fixed annuity.
We'd choose to devote a portion of our portfolio to an annuity if our required annual income is met (portfolio withdrawals +
annuity payments) and, after umpteen years, we have more money in our portfolio than if we hadn't chosen to buy the annuity.
We consider the following:
- We have $P0 and we're considering using some to buy a Life Annuity and the rest we'll invest.
-
The Annuity pays a fixed amount each year, namely a fraction r
of the purchase price of the Annuity.
(We'll call r the Annuity Rate.) - We'll devote a fraction f of our $P0 to buy this Annuity.
- This fraction will give us a constant C = r f P0 dollars every year.
- Our income needs increase each year. We need A1 in the first year, A2 in the second year, A3 in the third etc. etc.
- The annual Gain Factors for our investments are g1 in the first year, g2 in the second year, g3 in the third etc. etc.
- At the start of each year we withdraw from our Portfolio the income we need for that
year LESS the fixed Annuity, C
... except that we'll ignore this fixed Annuity ... for the moment:
| start of Year | Portfolio | Withdrawal | Balance = Portfolio - Withdrawal |
| 1 | P | A1 | P - A1 |
| 2 | P g1 -A1g1 | A2 | P g1 -{A1g1+A2} |
| 3 | P g1g2 -{A1g1g2+A2g2} | A3 | P g1g2 -{A1g1g2+A2g2+A3} |
| ... | etc. | etc. | etc. |
| N |
P g1g2...gN-1 -{A1g1g2...gN-1+A2g2...gN-1+...+AN-1gN-1} | AN |
P g1g2...gN-1 -{A1g1g2...gN-1+A2g2...gN-1+...+AN-1gN-1+AN} |
The final Portfolio (after N years) is the balance at the start of year N (as given in the above table) multiplied by the Gain Factor for year N, namely gN:
Final Portfolio(no annuity) = P g1g2...gN - {A1g1g2...gN+A2g2...gN+...+AN-1gN-1gN+ANgN}
For sanitary reasons, we'll let Gn be the cumulative Gain Factor over n years. That is, Gn = g1g2...gn.
That'll allow us to rewrite like so:
| Final Portfolio(no annuity) = GN [ P - {A1 +A2/G1 +A3/G2 +... +AN/GN-1} ] |
The starting Portfolio is P
and we now
consider taking out a fraction f of our initial money pot, P0,
to buy an Annuity
so our initial portfolio investment becomes P = P0 (1 - f)
and our annual withdrawals are all reduced by the Constant Annuity:
C = r f P0
so every Ak is changed to
Ak - r f P0 and we have, finally:
| [1]
Final Portfolio(with annuity)
= GN [
P0 (1 - f)
- {A1 +A2/G1 +A3/G2 +... +AN/GN-1}
|
If we put f = 0 we get the Final Portfolio without buying an Annuity (as noted earlier).
To see the conditions under which buying an Annuity would increase the Final Portfolio,
we look at the coefficient of f and insist that it be positive.
That results in the condition:
| Annuity Rate = r > 1 / {1+1/G1+ 1/G2+ ... +1/GN-1} |
|
Note that this condition is dependent only upon the Annuity Rate compared to
nominal Investment Returns and not upon the withdrawal amounts - it's independent of inflation*. 
Figure 1 | 
Figure 2 |
Stare at Fig. 2, above.
For the period 1960 - 2000, an S&P 500 Portfolio would benefit from an annuity if the annuity paid more than (about) 8%. Using the actual inflation and return figures, here's the picture for an initial $100K portfolio from which we need $5K per year (changing with inflation) and we use a fraction of the $100K to buy an annuity which pays R% (thereby reducing the amount withdrawn from the reduced portfolio to something less than $5K, initially).


|
On the other hand, if we're excited about a 9% annuity,
we'll have to wait 25 years before we see the benefits. Until then, although the initial portfolio has been reduced, the reduction in withdrawal amounts allow the reduced portfolio to grow.
In the early years, the $5000 income requirement is satisfied, Without the annuity the withdrawal rate is $5000 from $100K, namely 5%.
With 40% of the $100K devoted to a 9% annuity, the annuity income is a fixed $3600 and
the (initial) withdrawal rate is just $5000 - $3600 = $1400 from $60K, namely 2.3%. |

|
Let's look more closely at the formula [1] above, except that we'll assume:
- We begin with a $1.00 portfolio so P0 = 1. A fraction f of P0 will be used to buy an annuity.
- Then the initial income required, A1, as a fraction P0, is just the initial withdrawal rate, say W.
- We assume that the annual withdrawals increase at inflation rates i1, i2 ...
- Let Ik=(1+ik)(1+i2)...(1+ik) be the cumulative Inflation Factor, so our required incomes are W, I1W, I2W ...
- We make our final withdrawal at the end of year N ... so that makes N+1 withdrawals.
(That means we include a final term in formula [1].)
[2]
where:
|
Our formula then becomes:
Final Portfolio(with annuity) = GN[(1-f)-WgMS(I,N) + r f gMS(1,N)]
Note that the second gMS does NOT involve inflation!
We now compare the final portfolio, after N years, without and with an annuity:
Without Annuity:
Final Portfolio(without annuity) = GN[1-WgMS(I,N)]
Normally, we'd want our final portfolio without an annuity to survive N years.
That would require that
WgMS(I,N) < 1.
Remember that gMS(I,N) =
1+I1/G1+I2/G2+... +IN/GN
is increasing, as the years go by (as in Figure 1, above).
However, inflation may be large and/or the annual gains small so that
gMS may become large and, eventually,
WgMS(I,N) may exceed "1".
Suppose that (heaven forbid!) our Final Portfolio(without annuity) goes to $0 (at year N).
That means that:
| [a] Portfolio (without annuity) goes to $0 as soon as : gMS(I,N) > 1/W |
With Annuity:
Final Portfolio(with annuity) = GN[(1-f)-WgMS(I,N) + r f gMS(1,N)]or
Final Portfolio(with annuity) = Final Portfolio(without annuity) + f GN[ r gMS(1,N) - 1]Suppose that gMS(I,N) > 1/W so that, according to [a] above, the Final Portfolio(without annuity) = $0.
The big question is now: How does our Final Portfolio(with annuity) fare?
It would be interesting to know whether r gMS(1,N) > 1, eh?
That'd mean that we'd still have some Portfolio(with annuity) left when the Portfolio(without annuity) drops dead.
Now gMS(I,N) > gMS(1,N) since the inflation factors are greater than 1.
Suppose we could prove that gMS(I,N) < R gMS(1,N) for some value of R.
That means that
1/W < gMS(I,N) would make
1/W < R gMS(1,N)
= {R/r} r gMS(1,N).
Hence we'd have: r gMS(I,N) >
r/RW.
Hence we could guarantee that
r gMS(I,N) > 1, so long as
r > RW.
In other words, our Portfolio(with annuity) would survive beyond the point where the Portfolio(without annuity) drops dead provided we can find an annuity which pays at a rate greater than RW.
For example, if inflation is zero, then we can choose R = 1 so we need only have r > W (example: r > 4%).
Okay, we need to find R such that: gMS(I,N) < R gMS(1,N).
In other words, we need:
1+I1/G1+I2/G2+... +IN/GN <
R [1+1/G1+1/G2+... +1/GN].
In other words, we need:
[b] R-1+(R-I1)/G1+(R-I2)/G2+... +(R-IN)/GN > 0.
This will be satisfied if R > Ik for every k = 1, 2, 3, ... N.
In particular, if inflation is always positive, we can choose R > IN, the largest of the N inflation factors.
That means that if, over N years, the consumer price index (as a measure of inflation) grows by a factor of 2.3, then the
Portfolio(with annuity) will survive the Portfolio(without annuity) provided r > 2.3W.
For a withdrawal rate of 4%, this is guaranteed if Annuity Rate: r > 2.3*4% = 9.2%.
Of course, the value of R that we chose above was overkill (and therefore suggests a larger-than-required Annuity Rate).
The condition that R must satisfy is:
R > gMS(I,N) / gMS(1,N)
which can be rewritten as:
R > [ 1+I1/G1+I2/G2+... +IN/GN ] / [ 1+1/G1+1/G2+... +1/GN] = [ΣIk/Gk] / [Σ1/Gk]
which is a weighted average of the cumulative inflation factors Ik, the weights being 1/Gk.
These weights are greatest when the cumulative gain factors Gk are smallest. That (normally) occurs
in the first few years.
To get a feel for the required size of R we'll consider a constant inflation rate, i, so Ik = (1+i)k.
We'll also assume that the annual gain factors gk are (1+r) where r is the expected annualized return.
That'd make Gk = (1+r)k.
Then we'd get R >
[ΣIk/(1+r)k] /
[Σ1/(1+r)k] the sums going from k = 0 to k = N.
To get the largest R-value, we let N 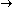 infinity. This gives R >
[1/{1-I/(1+r)}] /
[1/{1-1/(1+r)}] = r/(1+r-I) = r/(r-i).
infinity. This gives R >
[1/{1-I/(1+r)}] /
[1/{1-1/(1+r)}] = r/(1+r-I) = r/(r-i).
... using the fact that the infinite sum 1+x+x2 + ... is 1/(1-x).
Hence, we have an estimate of the Annuity Rate required so that
Portfolio(with annuity) outlasts the Portfolio(without annuity), namely:
r > r/(r-i)W.
For example, suppose we have $1M and we want $40K per year income.
That $40K is 4% of our initial monies, so W = 0.04.
If the expected annualized return for our portfolio is r% = 7%
and inflation is a constant at i% = 3%, then with an income requirement of
W = 4.0% (increasing with inflation), we'd need:
Annuity Rate = r > (r/(r-i))W = 7/(7-3)(4.0)% = 7%.
If we could get this rate, a Portfolio(with annuity) will outlast a Portfolio(without annuity).
| Indexed Annuities |
Okay, now we suppose that the annuity income is indexed to inflation.
That'd mean that, for a $1.00 portfolio, the annual income stream is: C = r f the first year,
but C I1 the next year, then C I2, C I3, etc.
The portfolio balance after N years would then be:
[3]
where:
|
Note that a portfolio without an annuity would have f = 0.
In order that the portfolio balance with an indexed annuity exceed the portfolio without, we'd need:
r > 1 / ΣIk/Gk.
Since the values of Ik are expected to be greater than 1, this is a number smaller than 1 / Σ1/Gk.
That is, the annuity rate to make an indexed annuity worthwhile is smaller than that required for a fixed annuity.
Compare (using 1960-2000 data):


Note that, for investments that provide big returns, you'd need a large annuity rate (either fixed or indexed)! 
Note, too, that without an annuity (either fixed or indexed), the rate of withdrawal from your portfolio (in order that your portfolio last exactly N years)
is given by: W = 1 / ΣIk/Gk. In other words, if you expect to withdraw x%
(increasing with inflation) and have your portfolio last until you drop dead, then it's worthwhile to buy an indexed annuity if the annuity rate exceeds x%. 
A spreadsheet that compares portfolios with and without annuities is described here.
