| XIRR and YTD : Part II ... continuation of Part I |
We're looking at Year-to-Date (YTD) returns and how they can go up even when your investment is buried under your pillow.
>Assuming you've already made some gains ... and then stick the money under the pilow, right?
Yes, but YTD is useful if you're talking about a stock or mutual fund.
If the YTD is 5.67% by April 30, it means $100 invested on Jan 1 would be worth $105.67 by April 30.
>So it's useful when you're talking about a single investment made on Jan 1, right?
Right, again.
|
Remember the situation we discussed in Part I?
We invest $10K on Jan1, withdraw $9K on Feb 1 leaving a portfolio balance of $1500. Thereafter, the return is 0% ... as though we put the $1500 under a pillow. The annualized return, calculated via Excel's XIRR function, decreases as the months go by, but the YTD return increases. The situation is illustrated in Figure 1. >And they're equal at 12 months.
| 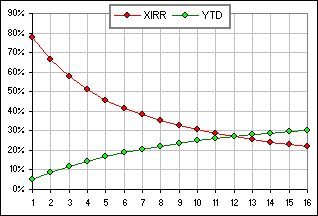 Figure 1 |
We start with $A on Jan 1 and, m months later, we withdraw a fraction w (that means we withdraw $wA).
After N months, our portfolio is worth a fraction b of our original portolio (so we're left with $bA).
If the compound monthly growth rate (CMGR) is called x (where x = 0.045 means a 4.5% rate), then x satifies:
[1a] A (1+x)N - wA (1+x)N-m = bA
or
[1b] (1+x)N - w (1+x)N-m = b
If we solve for x we'd get the CMGR.
However, the YTD gain factor is (1+x)N so the YTD rate is (1+x)N - 1 
YTD is what'd happen to a single investment made on Jan 1.
>And does that tell us why the YTD increases?
Yes. If we write [1b] like so:
[2] (1+x)N = b / [1 - w (1+x)-m]
Notice that, as we increase the number of months (that's N), the CAGR (that's x) will naturally decrease (since the final portfolio value stays fixed at $bA)
Now stare intently at [2] and you'll see that the right side increases as x decreases.
Hence, even though the monthly rate, x, decreases, the YTD increases with N.
>Why not look at the left side? After all, that's the YTD.
If x decreases and N increases, what happens to (1+x)N?
| Calculating YTD |
Suppose you've calculated the YTD-gain over N months (using, say, the XIRR ... or whatever).
Suppose you've also calculated YTD-gain over the next k months.
Then you'd think that you could get the YTD-gain over all N+k months by multiplying them together, right?
>Sure.
Consider, again, [1b] above:
[1b] (1+x)N - w (1+x)N-m = b
Remember that we're talking about an N-month time period, where our original $A portfolio winds up having the value $bA.
>And we've withdrawn $wA after m months, right?
Right, and x is the compound monthly growth rate based upon that N-month time period.
And
(1+x)N is the N-month gain factor and (1+x)N -1 is the N-month YTD return.
Note that, for small values of x, (1+x)N ≈ 1 + Nx so YTD is roughly N x.
Now suppose that ...
>YTD, the N-month rate, is roughly N times the monthly rate x, right?
Yes. Now suppose that we invest our final portfolio, namely $bA, for another k months at a monthly return of r.
We'd expect our new CMGR over N+k months to differ from the value x
... which was over N months.
We'll call the new rate y. To find y, we'd have to solve ...
>Wait! The YTD gain over the first N months is (1+x)N. We already know that.
Now we go another k months at a return of r. The gain for that time period would be (1+r)k.
Then the gain factor over all N+k months would be (1+x)N(1+r)k, right?
Sometimes ... if you're lucky it'd be that easy.
Note that the magic equation (to solve for y) is just like [1b],
except that our final portfolio has increased by the factor (1+r)k, giving:
[1c] (1+y)N+k - w (1+y)N-m+k = b(1+r)k
Suppose that we hadn't withdrawn any money, so w = 0. Then [1b] and [1c] would read:
[1b*] (1+x)N = b ... which is the N-month YTD.
[1c*] (1+y)N+k = b(1+r)k ... which is the YTD over N+k months.
If we divide [1c*] by [1b*] we can get: (1+y)N+k = (1+x)N(1+r)k.
>See? I told you! Just multiply the YTD for each time period ... and that's (1+x)N(1+r)k.
Aah, but that's with no withdrawals.
But, with that withdrawal stuck in there, would you say that y, the solution to
[1c], is satisfies (1+y)N+k = (1+x)N(1+r)k?
>Sure. Why not?
Okay, let's rewrite [1c] like so:
[1d] [ (1+y)N+k] - w [ (1+y)N+k](1+y)-m = b(1+r)k
Now stick (1+y)N+k = (1+x)N(1+r)k into [1d] and ask:
Is [(1+x)N(1+r)k]
- w [(1+x)N(1+r)k](1+y)-m = b(1+r)k ??
or, equivalently, is
[1e] (1+x)N
- w (1+x)N(1+y)-m = b ??
>Uh ... I give up.
Let me remind you of the equation that x satisfies: [1b] (1+x)N - w (1+x)N-m = b
or
[1b] (1+x)N - w (1+x)N(1+x)-m = b
See? [1e] and [1b] are the same equation, provided if x = y.
Remember: we want to see if (1+y)N+k = (1+x)N(1+r)k is valid.
We conclude that if all returns are the same, x = y = r, then we can just multiply our YTDs together.
Remember that x and y are compound monthly growth rates:
x is based upon the first N months, r on the next k months and y on all N+k months.
>I think that's important enough for ...
Quite right:
the monthly return over the next k months is r, then the YTD gain factor over all N+k months is: (1+YTD[N+k]) = (1+YTD[N])(1+r)k provided the compound growth rates are the same over each time period |
>Don't withdraw any money from your portfolio?
Why not?

Here's somethin' else to remember:
|
The XIRR value is the (constant) annual interest a (fictitious) bank would pay so that your deposits and withdrawals yield your final portfolio after one 365-day year.
If XIRR = 8.25% then a single $1000 deposited in that (fictitious) bank would give $1082.50 at the end of a year. That $1000 would grow to 1000 (1.0825)1/365 = $1000.22 in one day. That $1000 would grow to 1000(1.0825)123/365 = $1027.07 in 123 days (from Jan 1 to May 3). That same (fictitious) bank would turn $1000 deposited on Jan 1 into $1027.07 by May 3. That means that, if there were a single deposit of $1000, you'd have $1027.07 by May 3. (Forget deposits & withdrawals. We're talking a single deposit.) That means a 2.707% increase in 123 days. That means YTD = 2.707% on May 3. Moral?
|
| about XIRR and leap years |
Excel's XIRR function has the form: XIRR(cash flows, dates)
Aah, but when Excel calculates XIRR, it assumes a year has 365 days 
Nevertheless, (1+XIRR)^(1/365) will give the correct daily gain factor
... even in a year with 366 days !
To calculate a YTD return over N days, you can calculate: XIRR(cash flows, dates)
where the dates cover the N days
... then use: YTD = (1+XIRR)^(N/365) - 1.
... even in a year with 366 days !
Now try N = 366 ... as in (1+XIRR)^(366/365) - 1
Will you get the 366-day "annual" return for a leap year?
NO !
You'll get the "correct" daily gain factor ... that's (1+XIRR)^(1/365)
but (alas) it'll be applied to a 366-day interval hence it'll be too large

>If Excel thinks a year is always 365 days, then you should get the correct annual return for N = 365, right?
Sure, so can you calculate (1+XIRR)^(365/365) - 1 ?
>Wait'll I get my calculator ...
