| Ito Math ... an appendix to Part II |
| First we have to consider the ordinary, garden-variety Riemann Sum ...
>Huh? Patience. A Riemann Sum goes like so:
Each term, like f(tk)Δt, represents a rectangular area (as shown in dark green, in Figure 1). If we make the subintervals shorter and shorter, meaning that Δt is made smaller and smaller,
then (as seen in Figure 2), the sum of all the rectangular areas (that's our Riemann Sum) approaches ...
|  Figure 1
|
|
We need one other thing:
[f(tk+1) - f(tk)] / Δt is the slope of the chord,
from the point where t = tk However, if f(t) is a smooth (i.e. differentiable) function, then it's also the slope of the tangent at some point
between tk and tk+1. Such a point is labelled sk in Figure 3. That means ...
| 
Figure 3 |
We'll consider the following sum, called the Quadratic Variation of the function f on the interval [0,T]:
[f(t2) - f(t1)]2 + [f(t3) - f(t2)]2 + [f(t4) - f(t3)]2 + ... + [f(tn) - f(tn-1)]2 = Σ [f(tk+1) - f(tk)]2
Write
[f(tk+1) - f(tk)]2 =
[f '(sk)Δt] 2
and we get:
Σ [f(tk+1) - f(tk)]2 =
Σ[f '(sk)Δt] 2
= Δt Σ f '(sk)2Δt
As Δt 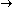 0 we get:
Σ f '(sk)2Δt
0 we get:
Σ f '(sk)2Δt
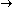
 f '(t)2 dt
and (of course!) Δt
f '(t)2 dt
and (of course!) Δt 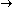 0
0
hence you can guess what their product approaches ...
If f(t) is a smooth (differentiable) function on [0,T], then
Σ [f(tk+1) - f(tk)]2 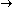 0
as Δt 0
as Δt 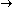 0 0
|
>So? Is that good?
It's to be expected, since that little guy, Δt , appears squared. One of them is incorporated into the Integral and the other ...
>Makes the result zero?
Yes. For smooth functions, the Quadratic Variation is zero.
>Is that good?
Well, the remarkable thing is this:
If f(t) is stochastic function, its Quadratic Variation is NOT zero !
>Wow! Uh ... is that good?


